Dr. Kumar Eswaran, a Hyderabad-based physicist, has appartently found a solution to the 161-year-old Riemann’s mathematical problem. The famous Riemann hypothesis is considered to be one of the seven unsolved mathematical problems. 

It was declared a millennium problem in 2000, by the Clay Mathematics Institute of Cambridge, with a reward of $1 million for anyone who solves it. Riemann Hypothesis was first posited by Bernhard Riemann in 1859. 

Riemann Hypothesis fundamentally helps to count prime numbers and provides a method to generate large random numbers. In simple words, it deals with understanding the distribution of prime numbers. The Riemann Hypothesis originated from the work of well-known mathematician Carl Friedrich Gauss in the 19th century. 

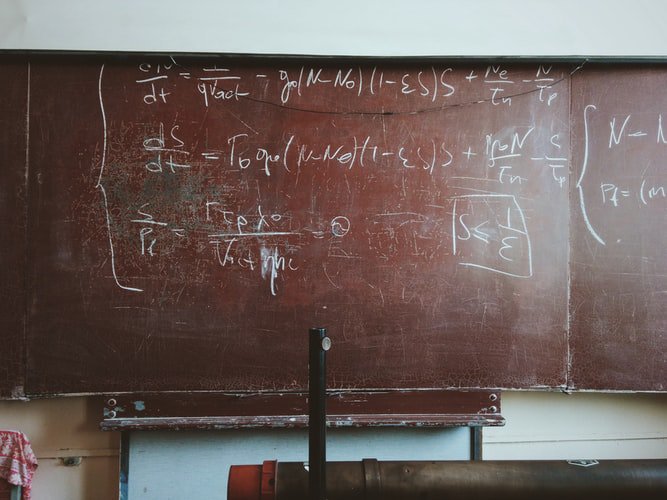
Kumar Eswaran, a mathematician from Sreenidhi Institute of Science and Technology, Hyderabad, placed the research title as “The final and exhaustive proof of the Riemann Hypothesis from first principles” five years ago on the internet. 

Unsplash

Dr. Kumar Eswaran informed Deccan Chronicle, “It was, in fact, back in 2016, that I first gave proof for the formula improved by the great mathematician George Friedrich Bernhard Riemann in the 1800s. I had put it on the web for open review and downloads after working on it for about six weeks. During 2018-19, I gave several lectures on the proof.”

According to the experts, solving the Riemann Hypothesis opens up opportunities for the use of prime numbers in cryptography and impacts the number theory. After due research since February 2020, following thousands of downloads on the internet, an expert committee consisting of eight mathematicians constituted to study the proof by Dr. Kumar Eswaran. 

news18

Eswaran told Times of India, “While one can easily count the number of prime numbers from say 1-20, it becomes a tedious task to calculate the number of prime numbers till one million or 10 billion. The hypothesis was important to prove as it would enable mathematicians to exactly count the prime numbers.” While the expert committee has invited more than 1,200 mathematicians to participate in the open review, and seven international scholars have responded.

Professor M Seetharaman, from the department of theoretical physics at the University of Madras, who was one among many who reviewed the Riemann Hypothesis proof by Eswaran, told Times of India, “The author’s analysis is exhaustive, unambiguous and every step in the analysis is explained in great detail and established. The conclusions of the author and his result must therefore be considered proven.”